Forenzika izbora u realnom vremenu: Klimekove kumulativne krive

Detekcija anomalija u obrascima izlaznosti i podrške korišćenjem kumulativnog rasporeda

Uvod

Jedan od najzapaženijih doprinosa izbornoj izbora u poslednjoj deceniji jeste rad Petera Klimeka i saradnika iz Medicinskog univerziteta u Beču, koji su razvili pristup zasnovan na kumulativnim krivama izlaznosti i glasova po biračkim mestima.

Njihov metod je elegantan, ali izuzetno snažan: kada se biračka mesta poređaju po izlaznosti i prikaže se kako se akumulira ukupan broj glasova za određenog kandidata, normalan izborni proces proizvodi glatku, kontinuiranu „S“ krivu. Suprotno tome, manipulisani izbori proizvode zakrivljenja i nagle skokove, koji se vizuelno lako uočavaju.

Ovaj metod se pokazao posebno efikasnim u analizama izbora u Rusiji i Iranu, i koristi se kao dokazni alat u akademskim i pravnim analizama izbornih manipulacija.

Intuitivno objašnjenje

Zamislite da imate listu svih biračkih mesta i da za svako znate:

izlaznost (%),
broj glasova za kandidata A.

Ako poredite mesta po rastućoj izlaznosti i za svako sabirate glasove za kandidata A, trebalo bi da dobijete glatku krivu, jer u demokratskom procesu nema razloga da mesta sa visokom izlaznošću automatski daju nesrazmerno mnogo glasova.

Ali ako poslednjih 10% mesta sa ekstremnom izlaznošću donosi 30% svih glasova za jednog kandidata, to je signal da je izlaznost i broj glasova, manipulisani.

Teorijska osnova

Postupak je sledeći:

Sortiramo biračka mesta po izlaznosti \(T_i\) (npr. od 0% do 100%).
Za svako mesto imamo i broj glasova za određenog kandidata \(V_i\).
Izračunavamo kumulativne sume:

\(C_T(k) = \sum_{i=1}^{k} T_i, \quad C_V(k) = \sum_{i=1}^{k} V_i\)

Crtamo \(C_V(k)\) protiv \(C_T(k)\), pa dobijamo kumulativnu krivu.
U regularnim izborima, ova kriva ima konveksan, stabilan oblik. U manipulisanima, primećuju se iznenadni skokovi u visokoizlaznim mestima, odn. odsustvo nivoa saturacije/zasićenja.

Tipovi manipulacija koje otkriva

Klimekova metoda je usmerena na:

Ubacivanje listića za jednog kandidata u visokoizlaznim mestima
Nesrazmernu podršku u mestima sa gotovo 100% izlaznošću
Proizvoljno dodeljivanje glasova u „tvrđavama“ režima
Neprirodnu koncentraciju podrške u delu distribucije

Primena u Excel-u i R-u

📊 U Excel-u:

Uneti podatke po biračkom mestu: izlaznost, broj glasova za kandidata.
Sortirati po izlaznosti.
Napraviti kumulativnu sumu izlaznosti i glasova.
Prikazati grafik Kumulativni glasovi protiv Kumulativna izlaznost.

📈 U R-u:

Kao u prethodnoj ilustraciji:

set.seed(303)
vreme <- seq(7, 20, by = 1)
normalna <- cumsum(c(2.5, 3, 2.5, 3, 2.5, 3, 2, 2, 1.5, 1, 1, 0.8, 0.7, 0.5))
manipulisana <- cumsum(c(2.5, 3, 2.5, 3, 2.5, 3, 2, 2, 2, 5, 5, 3, 2, 1.5))
df <- data.frame(vreme, normalna, manipulisana)

df_long <- tidyr::pivot_longer(df, cols = c("normalna", "manipulisana"), names_to = "tip", values_to = "izlaznost")

ggplot(df_long, aes(x = vreme, y = izlaznost, color = tip)) +
  geom_line(size = 1.2) +
  scale_color_manual(values = c("steelblue", "red"), labels = c("Sumnjiva", "Očekivana")) +
  labs(
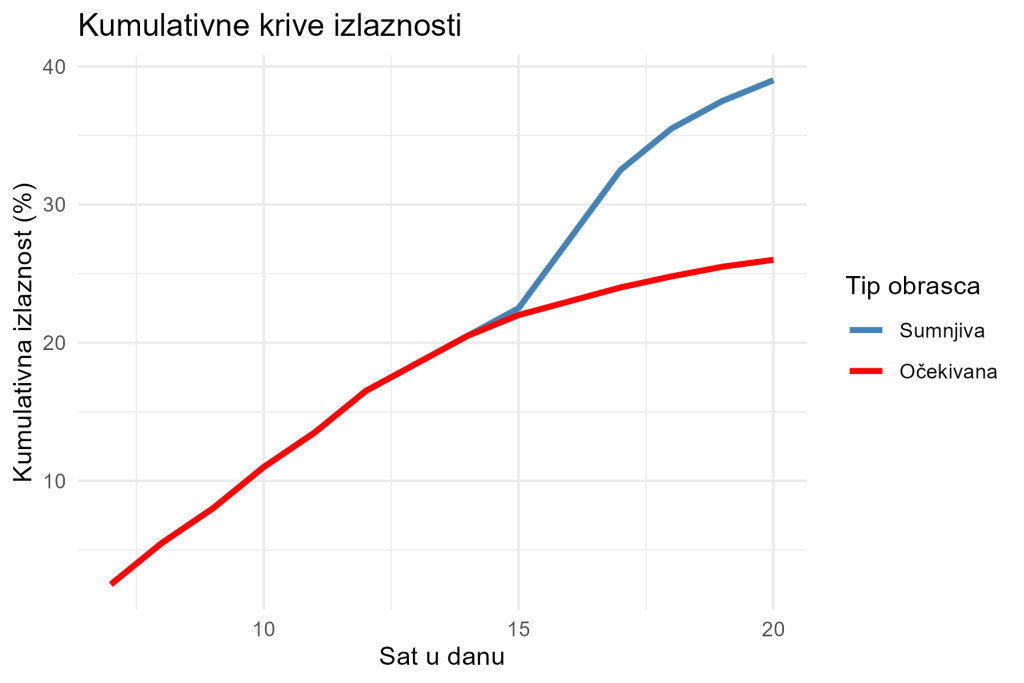
    title = "Kumulativne krive izlaznosti",
    x = "Sat u danu",
    y = "Kumulativna izlaznost (%)",
    color = "Tip obrasca"
  ) +
  theme_minimal()

Ova kumulativna kriva vizualizuje razliku između regularnog i sumnjivog toka glasanja. Slika 1 ilustruje tu razliku.

Realna primena i referenca

🟥 Rusija (2011, 2012):

Klimek i saradnici su identifikovali da poslednjih 10–20% biračkih mesta sa ekstremno visokom izlaznošću donosi nesrazmerno visok broj glasova za vladajuću stranku. Ovo je korišćeno kao jedan od ključnih dokaza za sistemsku manipulaciju.

Referenca:

Klimek, P., Yegorov, Y., Hanel, R., & Thurner, S. (2012). Statistical detection of systematic election irregularities. PNAS, 109(41), 16469–16473. DOI: https://doi.org/10.1073/pnas.1210722109

Zaključak

Klimekove kumulativne krive su vizuelno intuitivne, lako primenljive i izuzetno moćne za detekciju neprirodnih obrazaca u izborima. One ne samo da pokazuju da je neka neregularnost prisutna, već ukazuju i gde u distribuciji se dešava, i to na način koji je lako komunicirati široj javnosti, pravnicima, novinarima i drugim posmatračima.

U kombinaciji sa prostornim i vremenskim analizama, predstavljaju snažan alat za evaluaciju izbornih rezultata u realnom vremenu.