1. Uvod: Zašto regresija u forenzici izbora?

Regresiona analiza je metod kojim se procenjuje kako se zavisna promenljiva menja pod uticajem jedne ili više nezavisnih promenljivih. Za razliku od korelacije, koja meri samo povezanost između promenljivih, regresija nam daje kvantitativnu meru uticaja i omogućava procenu u kojoj meri objašnjavajuće promenljive doprinose rezultatu.

U kontekstu izbora, regresija se može koristiti za ispitivanje pitanja poput:

• Da li povećana izlaznost doprinosi rastu glasova vladajuće stranke?
• Koji je uticaj glasanja izvan biračkog mesta na rezultate?
• Kako nevažeći listići utiču na procenat osvojenih glasova?
• Kako istovremeno izlaznost, mobilno glasanje i nevažeći listići utiču na procenat osvojenih glasova?

---

2. Linearni regresioni modeli

Jednostavna regresija – intuitivna osnova

Jednostavna regresija je najintuitivniji oblik regresione analize. Možemo je zamisliti kao pokušaj da se utvrdi koliko jedan faktor utiče na rezultate. Na primer, ako posmatramo odnos između izlaznosti i glasova za vladajuću stranku, jednostavna regresija nam pomaže da procenimo da li veća izlaznost znači i veći udeo glasova za tu stranku. Za posmatrače i analitičare, ovakav pristup je koristan jer omogućava da se proveri da li povećana izlaznost deluje neutralno ili daje nesrazmernu korist jednoj strani. Ukoliko se pokaže da je izlaznost snažno povezana samo sa glasovima vladajuće partije, to može biti signal za dodatnu pažnju i istraživanje nepravilnosti.

U jednostavnoj regresiji postoji jedna nezavisna promenljiva. Model može izgledati ovako: \(Y = \alpha + \beta X + \varepsilon \)

Primer: \(Y\) = procenat glasova za SNS, \(X\) = izlaznost.

• Ako je \(\beta = 0,5\), to znači da svaki dodatni procenat izlaznosti povećava udeo glasova za SNS za 0.5 procentnih poena.
• Ako je \(R^2 = 0,8\), to znači da 80% varijacija u glasovima SNS-a može da se objasni izlaznošću.

Ilustrativni primer – Rezultat regresije:

\(\%\text{SNS} = 20+0,6 \times \text{Izlaznost} \quad R^2 = 0,75 \)

• \( \beta = 0,6\) → kada se izlaznost poveća za 1 pprocentni poen, udeo glasova SNS raste za 0.6 procentnih poena.
• \(R^2 = 0,75\) → izlaznost objašnjava 75% varijacija udela osvojenih glasova SNS, što je vrlo jak odnos.

Kada se na istom grafikonu prikažu regresione linije za vladajuću i opozicionu partiju, posmatrači mogu jasno da uoče obrasce koji ukazuju na potencijalnu manipulaciju. U normalnim okolnostima očekivali bismo da veća izlaznost proporcionalno utiče na sve političke aktere, dakle, da se sa porastom izlaznosti povećava i udeo glasova i vlasti i opozicije, ili da takve promene budu statistički zanemarljive. Međutim, u kontekstu izbornih nepravilnosti često se dešava da regresiona prava vladajuće partije ima pozitivan nagib, što znači da se njen rezultat povećava sa rastom izlaznosti, dok opoziciona partija pokazuje negativan nagib, sa većom izlaznošću njen udeo opada. Ovakav obrazac sugeriše da dodatno mobilisani glasači nisu neutralni, već da su ciljano „usmereni“ ka podršci vlasti, dok opozicioni birači ne učestvuju u istom stepenu. Za posmatrače izbora, ovo je posebno važan signal jer ukazuje na instrumentalnu mobilizaciju i mogućnost da je izlaznost kontrolisana ili pritisnuta u korist vladajuće stranke.

Na istom grafikonu prikazane su regresione linije za vladajuću (plava) i opozicionu partiju (crvena). U slučaju izborne manipulacije očekuje se pozitivan nagib za vladajuću partiju, sa rastom izlaznosti raste i njen udeo glasova, dok opoziciona partija pokazuje negativan nagib, što znači da sa većom izlaznošću njen rezultat opada.

Analiza slučaja: Predsednički izbori u Ruskoj Federaciji (2004 i 2008) i Srbiji 2022.

Ruski forenzičari izbora koristili su regresiju osvojenih glasova prema izlaznosti da bi pokazali izborne manipulacije na predsedničkim izborima u Ruskoj Federaciji. Regresiona prava kandidata Putina ima izražen pozitivan trend (Slika 2), dok regresiona prava drugog kandidata Haritonova je praktično paralelna sa horizontalnom osom. Znači da sa povećanjem izlaznosti jedino kandidat Putin ima korist, dok se udeo glasova drugog kandidata ne menja sa porastom izlaznosti. Slična situacija se ponovila i 2008. godine, ali sada sa Medvedevim kao predsedničkim kandidatom.

Slika 3. ilustruje slične obrasce ponašanja na predsedničkim izborima u Srbiji 2022. godine u Topličkom okrugu. Regresiona prava u slučaju kandidata Vučića ne samo da ima statistički značajno izražen pozitivan nagib (P vrednost je manja od 1%) nego je i koeficijent nagiba veći od jedan (1,13). To znači da je na svakih 100 birača ovaj kandidat dobio 113 glasova. Naravno, takav rezultat je nemoguć osim ukoliko nije bilo izbornih manipulacija. Koeficijent nagiba kod drugog kandidata je negativan (-0,0496) i statistički značajan (P vrednost je manja od 3%). To znači da se sa povećanjem izlaznosti udeo glasova ovog kandidata smanjuje.

---

Višestruka regresija – intuitivna osnova

Višestruka regresija ide korak dalje i omogućava da istovremeno posmatramo više faktora. Na izborima, rezultat stranke može zavisiti ne samo od izlaznosti, već i od učešća glasova van biračkog mesta, broja nevažećih listića, pa čak i od geografske lokacije biračkih mesta. Višestruka regresija može „odvojiti“ efekat svakog od ovih faktora i pokazati koji su stvarno značajni. Na primer, može otkriti da izlaznost sama po sebi nema značajan uticaj, ali da glasanje van biračkog mesta ima snažnu i konzistentnu vezu sa rezultatima vladajuće partije. Za posmatrače, ovo je dragoceno jer ukazuje na konkretne kanale kroz koje se izborni proces može manipulisati.

Višestruka regresija omogućava uključivanje više faktora odjednom.

\(Y = \alpha + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \varepsilon\)

Primer: \( Y\) = glasovi SNS; \(X_1\)= izlaznost, \(X_2\) = glasanje van biračkog mesta, \(X_3\) = broj nevažećih listića.

Ilustrativni primer: \(\%\text{SNS} = 45 + 0,16 \times \text{Izlaznost} + 1,2 \times \text{Mobilni} – 1,7 \times \text{Nevazeci}, \quad R^2 = 0,65\)

Toplotna mapa prikazuje ocenjene beta koeficijente u višestrukoj regresiji. Pozitivan koeficijent (crveno) znači da promenljiva povećava udeo glasova SNS-a, dok negativan koeficijent (plavo) znači da ga smanjuje. Ovakav prikaz pomaže posmatračima da vizuelno sagledaju koji faktori imaju najveći uticaj.

Kod višestruke regresije posmatramo istovremeno više faktora koji mogu uticati na rezultat. U našem primeru, pored izlaznosti uključeni su i procenat glasanja van biračkog mesta i broj nevažećih listića. Vizuelni prikaz beta koeficijenata jasno pokazuje koji faktori imaju pozitivan, a koji negativan uticaj na rezultat vladajuće partije. Pozitivni koeficijenti ukazuju na to da povećanje te promenljive vodi ka rastu glasova za vlast, dok negativni sugerišu suprotan efekat. Za posmatrače i analitičare ovakav grafikon je koristan jer omogućava da se brzo uoče kanali kroz koje vlast može sticati prednost – na primer, mobilno glasanje, kao i faktori koji potencijalno smanjuju njene rezultate, poput većeg broja nevažećih listića. U kontekstu forenzike izbora, ovakva analiza pomaže da se precizno identifikuju „kritične tačke“ izbornog procesa koje zahtevaju posebno nadgledanje.

3. Studija slučaja: Kosjerić i Zaječar (2025)

Kosjerić

Model: \(\%\text{SNS} = 30,53 + 1,66 \times \text{Mobilni} + 0,17 \times \text{Izlaznost}, \quad R^2 = 0,26\)

t-vrednosti za tri regresiona koeficijenta su 0,62, 2,79 i 0,29 respektivno.

Tumačenje:

• Izlaznost nema značajan uticaj (koeficijent statistički beznačajan).
• Mobilni glasovi su snažno značajni: +1 procentni poen mobilnih birača → +1,66 procentnih poena SNS glasova.
• \(R^2 = 0,26\) model objašnjava samo 26% varijacija, što znači da postoje i drugi nepoznati faktori.

Forenzičko tumačenje:
Glasanje van biračkog mesta predstavlja sistematski izvor prednosti za SNS. Ovi nalazi upućuju na manipulacije u procesima koje opozicija teško može da kontroliše.

---

Zaječar

Model: \(\%\text{SNS} = 50,25 + 1,16 \times \text{Mobilni} + 0,17 \times \text{Izlaznost} – 1,03 \times \text{Nevazeci}, \quad R^2 = 0,54\)

t-vrednosti za četiri regresiona koeficijenta su 4,17, 2,99, 0,46 i 3,79 respektivno.

Tumačenje:

• Izlaznost nema značajan uticaj (\(\beta = 0,17\), statistički beznačajno).
• Mobilni glasovi značajni: +1 procentni poen mobilnih birača → +1,16 procentnih poena udela SNS glasova.
• \(R^2 = 0,54\) → model znači da 54% varijacija u SNS rezultatima objašnjava ovaj model, solidna moć predviđanja.

Forenzičko tumačenje:
Model bolje objašnjava varijacije u SNS rezultatima u odnosu na kosjerićki model. Ponovo se potvrđuje da je glasanje van biračkog mesta ključno za rezultat SNS-a. Ova zavisnost sugeriše da manipulacije nisu izolovan slučaj, već obrazac.

4. Napredne regresione metode

Napredne varijante regresije služe za složenija pitanja. Logit i probit modeli koriste se kada nas zanima verovatnoća da se dogodi određeni izborni ishod, npr. da li vladajuća stranka prelazi 50% glasova na određenom biračkom mestu. Panel regresije koriste podatke kroz vreme i prostor i mogu da pokažu da li se obrasci manipulacija ponavljaju ili menjaju iz izbora u izbore.

Za posmatrače i istraživače, ovi modeli su posebno korisni jer omogućavaju da se pređu granice osnovne analize i postave preciznija pitanja o ponašanju birača i izbornim nepravilnostima. Na primer, logit/probit analiza može pokazati kako verovatnoća izborne pobede zavisi od učešća mobilnih glasova, dok panel analiza može otkriti da li se veza između izlaznosti i rezultata vladajuće stranke vremenom učvršćuje.

Logit i Probit modeli u forenzici izbora

Teorijski uvod

Kada želimo da analiziramo verovatnoću da se dogodi određeni ishod (npr. da vladajuća partija osvoji više od 50% glasova na biračkom mestu), linearna regresija nije pogodna jer može davati vrednosti manje od 0 ili veće od 1. Zato koristimo logit i probit modele, koji su posebno dizajnirani za binarne ishode.

• Logit model koristi logističku funkciju:

\(p= \frac{1}{1+e^{-(\alpha + \beta X)}}\)​

ili, ekvivalentno: \(\ln\!\left(\frac{p}{1-p}\right) = \alpha + \beta X\)

Dakle, umesto da regresija predviđa direktno verovatnoću, ona predviđa log-odds (logaritam šansi). Intuitivno objašnjenje i ilustracija ovog pokazatelja data je nešto niže.

• Probit model koristi standardnu normalnu distribuciju:

\(p = \Phi(\alpha + \beta X)\)

gde je \(\Phi\) kumulativna funkcija rasporeda standardnog normalnog rasporeda.

U oba slučaja, cilj je isti: da dobijemo procenu verovatnoće da se dogodi određeni ishod na osnovu objašnjavajućih faktora.

---

Intuitivna osnova

Logit model

Možemo ga zamisliti kao „prevođenje“ objašnjavajućih faktora (npr. procenat mobilnih glasova) u šanse (odds) da vladajuća partija pređe određeni prag. Svaki koeficijent \(\beta\) u logit modelu znači da se log-šanse povećavaju za toliko jedinica kada \(X\) poraste za 1.

Ako je \(\beta = 0.8\), šanse se povećavaju za faktor \(e^{0,8} \approx 2,23\). To znači da se šanse (odds) više nego udvostručuju sa svakim dodatnim procentnim poenom mobilnih glasova.

Probit model

Probit model koristi standardnu normalnu krivu u obliku zvona. Koeficijenti menjaju latentnu skalu, a verovatnoće se računaju pomoću normalne kumulativne funkcije. Intuitivno, probit i logit daju vrlo slične rezultate u praksi, ali logit ima jednostavniju interpretaciju kroz odds ratio, dok probit naglašava promene na latentnoj skali.

---

Intuitivno objašnjenje koeficijenata na simuliranom primeru

Zamislimo da analiziramo verovatnoću da SNS pređe 60% glasova na biračkom mestu.

Rezultati logit regresije (simulirani podaci): \(\ln\left(\frac{p}{1-p}\right) = -3 + 0.8 \times \text{Mobilni}\)

• Slobodni član (-3): Kada nema mobilnih glasova, log-odds su negativni, što znači vrlo mala verovatnoća da SNS pređe 60%.
• Koeficijent (0,8): Svaki dodatni procentni poen mobilnih glasova povećava log-odds za 0,8, što odgovara uvećanju šansi za oko 2,23 puta.
• Marginalni efekti:
  • Ako udeo mobilnih glasača raste sa 2% na 3%, verovatnoća raste sa ~0,11 na ~0,22.
  • Ako raste sa 5% na 6%, verovatnoća skače sa ~0,50 na ~0,65.
  • Ako raste sa 8% na 9%, verovatnoća ide sa ~0,88 na ~0,93.
    → Najveći efekat se javlja kod srednjih vrednosti.

Kod probit modela koeficijent ima sličnu interpretaciju, ali bez odds ratio; efekat se izražava kroz promenu u latentnoj z-vrednosti normalnog rasporeda, a u verovatnoće se prevodi pomoću \(\Phi\).

Jednostavno objašnjenje pojma šansi (odds) kroz fudbal i izbore

Pojam šanse (odds) najbolje razumemo kroz analogiju sa kladionicom. Kada kladionica objavi kvote da će Brazil osvojiti Svetsko prvenstvo (3:1), to znači da su šanse Brazila otprilike 25%. Ako je kvota za Srbiju 50:1, to znači da je verovatnoća svega 2%.

Slično tome, u forenzici izbora možemo posmatrati šanse da SNS pređe 50% u različitim opštinama (ilustrativni primer):

• Urbana opština: 3:1 protiv SNS-a (25% verovatnoće).
• Mešovita opština: 1:1 (50% verovatnoće).
• Ruralna opština: 1:4 za SNS (80% verovatnoće).

👉 Zaključak: Kao što kvote u sportu pomažu kladioničarima da identifikuju favorite i autsajdere, tako logit modeli u forenzici izbora pokazuju gde je vladajuća partija „favorizovana“ u izbornom procesu. Ako šanse za SNS naglo rastu sa porastom mobilnih glasova, to je signal da upravo ta kategorija glasanja može biti izvor nepravilnosti.

Još malo teorijskog objašnjenja šansi i odnosa šansi

Ako je verovatnoća nekog događaja \(p\), šansa tog događaja je definisana kao \(\frac{p}{1-p}\). Ako je šansa događaja u posmatranoj grupi \(\frac{p}{1-p}\), a šansa u drugoj grupi \(\frac{q}{1-q}\), tada je odnos šansi (eng. odds ratio) dat sa \(\frac{p}{1-p}/\frac{q}{1-q}\). Ako je \(p\) i \(q\) malo, tada će odnos šansi biti blizak relativnom riziku \(\frac{p}{q}\). No, odnos šansi i relativni rizik počinju da se razlikuju kada su apsolutni rizici veći od 20%.

Analiza slučaja: Zaječar 2025

Podaci lokalnih izbora 2025 u Zaječaru korišćeni za ocenu logit i probit modela mogu se ovde preuzeti:

Podaci sadrže sledeće promenljive: Izlaznost, SNS = procenat glasova koji je osvojio SNS, PUKV = procenat glasova koji je osvojila lista “Promena u koju verujemo“, Mobilni = broj glasova van biračkog mesta, Iznad60 je binarna promenljiva (1 ako SNS > 60% glasova, 0 inače) i Nevezeci = broj nevažećih listića.

✅ R

# Logit model
data <- read.CSV("izborni_podaci.CSV")
logit_model <- glm(Iznad60 ~ Mobilni + Izlaznost + Nevazeci, data=data, family=binomial(link="logit"))
summary(logit_model)

# Probit model
probit_model <- glm(Iznad60 ~ Mobilni + Izlaznost + Nevazeci, data=data, family=binomial(link="probit"))
summary(probit_model)

Dobijeni su sledeći rezultati:

# Logit model
Call:
glm(formula = Iznad60 ~ Mobilni + Izlaznost + Nevazeci, family = binomial(link = "logit"), 
    data = data)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  1.155745   2.933961   0.394    0.694    
Mobilni      0.083062   0.051025   1.628    0.104    
Izlaznost    0.003424   0.040476   0.085    0.933    
Nevazeci    -0.456446   0.114948  -3.971 7.16e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 92.747  on 66  degrees of freedom
Residual deviance: 49.292  on 63  degrees of freedom
AIC: 57.292

Number of Fisher Scoring iterations: 6

# Probit model
Call:
glm(formula = Iznad60 ~ Mobilni + Izlaznost + Nevazeci, family = binomial(link = "probit"), 
    data = data)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  0.337787   1.713486   0.197   0.8437    
Mobilni      0.046769   0.027613   1.694   0.0903 .  
Izlaznost    0.007397   0.023820   0.311   0.7562    
Nevazeci    -0.256323   0.058118  -4.410 1.03e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 92.747  on 66  degrees of freedom
Residual deviance: 49.440  on 63  degrees of freedom
AIC: 57.44

Number of Fisher Scoring iterations: 6

🔹 Rezultati logit modela

Mobilni      0,0831   p = ,104   (pozitivan, granično značajan)
Izlaznost    0,0034   p = ,933   (beznačajan)
Nevazeci    -0,4564   p < ,001   (negativan, vrlo značajan)

• Mobilni glasovi: koeficijent je pozitivan (0,08), što znači da sa svakim dodatnim procentnim poenom mobilnih glasova rastu šanse da SNS pređe 60%. Iako p-vrednost (,104) pokazuje da to još nije „statistički sigurno“ na 5% nivou, rezultat ide u smeru koji često viđamo kod manipulacija – mobilno glasanje „gura“ rezultat vlasti.
• Izlaznost: praktično nikakav efekat (p = ,93). To znači da izlaznost sama po sebi ne utiče na šanse SNS-a.
• Nevažeći listići: snažan negativan efekat (p < ,001). Što je više nevažećih listića, to su manje šanse da SNS pređe 60%. Drugim rečima, manji broj nevažećih ide u korist SNS-u. Ovo može značiti ili da je proces obrade glasova kontrolisan na način da se smanjuje broj nevažećih u korist vlasti, ili da opozicija ima više problema sa „pokvarenim“ listićima.

Vizuelizacija šansi: kombinovani efekti mobilnih i nevažećih glasova

Kada posmatramo logit modele, koeficijenti sami po sebi često deluju apstraktno. Zato je korisno prikazati rezultate u obliku grafikona koji jasno ilustruju kako se šanse vladajuće stranke menjaju sa različitim vrednostima ključnih faktora.

1. Efekat mobilnih glasova pri različitim nivoima nevažećih listića

Grafikon na Slici 5 prikazuje kako se verovatnoća da SNS osvoji više od 60% glasova menja sa rastom mobilnih glasova, uz različite nivoe nevažećih listića.

👉 Tumačenje: Što je veći procenat mobilnih glasova, to je veća verovatnoća da SNS pređe prag od 60%. Međutim, ova veza zavisi i od broja nevažećih listića, pri većem udelu nevažećih, verovatnoća značajno opada. Najpovoljniji scenario za SNS je kombinacija većeg broja mobilnih glasova i manjeg broja nevažećih.

2. Efekat nevažećih listića pri različitim nivoima mobilnih glasova

Drugi grafikon na Slici 6 pokazuje kako se verovatnoća da SNS pređe 60% glasova menja sa rastom nevažećih listića, za različite nivoe mobilnih glasova.

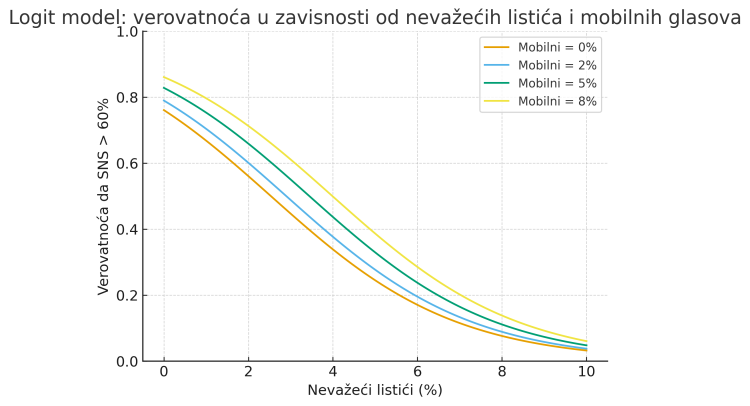
👉 Tumačenje: Sa porastom nevažećih listića, šanse SNS-a naglo opadaju. Ipak, tamo gde je broj mobilnih glasova visok, SNS i dalje ima znatno bolju poziciju. To pokazuje da se manipulativni efekat mobilnog glasanja može „suprotstaviti“ negativnom efektu nevažećih listića. Drugim rečima, vlast dobija na jednom kanalu (mobilni), ali gubi na drugom (nevažeći).

Šta ovo znači za posmatrače?

Ova dva grafikona zajedno jasno pokazuju da se ključne nepravilnosti u izbornom procesu mogu odvijati kroz upravljanje mobilnim glasanjem i tretmanom nevažećih listića.

• Ako vidimo visoke mobilne procente i niske nevažeće, SNS gotovo sigurno prelazi 60%.
• Ako su mobilni niski, a nevažeći visoki, šanse SNS-a se naglo smanjuju.
• Najsumnjiviji obrasci su oni gde SNS uspeva da istovremeno poveća mobilne glasove i „očisti“ nevažeće listiće.

Za posmatrače, to znači da fokus posmatranja mora biti dvostruk: kontrola mobilnog glasanja i kontrola procesa proglašavanja listića nevažećim.

🔹 Rezultati probit modela

Mobilni      0,0468   p = ,0903   (pozitivan, skoro značajan)
Izlaznost    0,0074   p = ,7562   (beznačajan)
Nevazeci    -0,2563   p < ,001    (negativan, vrlo značajan)

Probit daje istu priču:

• Mobilni glasovi su pozitivni i blizu značajnosti (što potvrđuje trend).
• Izlaznost nema nikakav efekat.
• Nevažeći listići imaju vrlo jak negativan uticaj.

---

🔹 Šta ovo znači u forenzici izbora?

1. Mobilno glasanje: pokazuje se kao faktor koji (najverovatnije) pomaže SNS-u. To potvrđuje ono što je čest nalaz u Srbiji, mobilni glasovi su kanali koji često favorizuju vlast.
2. Nevažeći listići: snažan indikator. Manje nevažećih listića → veće šanse SNS-a da pređe 60%. To može značiti da je postupak validacije listića vođen tako da se što manje glasova SNS-a proglasi nevažećim, ili da su glasači opozicije češće imali problem sa ispunjavanjem listića. Za posmatrače je ovo crvena zastavica, posebno treba proveravati kako se tretiraju nevažeći listići.
3. Izlaznost: ponovo nema značaja. To znači da „pumpanje“ izlaznosti nije presudan mehanizam, ključni kanali su mobilno glasanje i tretman nevažećih listića.

---

🔹 Kolike su šanse SNS-a da dobije preko 60% glasova?

U logit modelu, šanse (odds) zavise od konkretnih vrednosti ulaznih promenljivih. Ali iz slobodnog člana i koeficijenata možemo izvući osnovni zaključak:

• Kada nema mobilnih glasova i nema nevažećih listića, polazna tačka daje pozitivan log-odds (slobodni član ≈ 1,16), što odgovara šansama od oko 76% verovatnoće da SNS pređe 60%.
• Ako se udeo mobilnih glasova poveća, verovatnoća raste još više.
• Ako raste broj nevažećih listića, verovatnoća se naglo smanjuje (jer je njihov koeficijent snažno negativan).

Dakle: SNS u proseku ima više od 70% šanse da pređe prag od 60% glasova, ali ta šansa zavisi od dva ključna faktora, pozitivno mobilni glasovi, negativno nevažeći listići.

---

👉 Ukratko: Mobilni glasovi i kontrola nevažećih listića su glavni mehanizmi koji odlučuju da li SNS prelazi 60% glasova na biračkom mestu. Za posmatrače, ovo znači da pažnju treba usmeriti upravo na te dve kategorije, ko ima kontrolu nad mobilnim glasanjem i kako se klasifikuju nevažeći listići.

Praktične preporuke za posmatrače

Rezultati logit i probit analiza mogu biti izuzetno korisni posmatračima i analitičarima, ali samo ako se pravilno interpretiraju. Evo nekoliko ključnih preporuka:

1. Fokus na šanse, a ne na same procente.
   Logit i probit modeli pokazuju kako faktori menjaju šanse za određeni ishod (npr. SNS > 60% glasova), a ne samo koliko procenata raste ili pada rezultat. Ako šanse u pojedinim opštinama ili biračkim mestima izgledaju „nenormalno visoke“, to je signal da treba pojačati posmatranje.
2. Marginalni efekti su ključni za razumevanje.
   Koeficijenti sami po sebi nisu intuitivni, ali marginalni efekti (promene verovatnoće za +1 procentni poen promene u faktoru) daju jasnu sliku. Posmatrači treba da traže analize gde su koeficijenti prevedeni u konkretne promene verovatnoće.
3. Uporedite opštine i cikluse.
   Ako logit/probit analiza pokaže da u jednoj opštini šanse da SNS pređe 60% rastu sa 30% na 90% kada mobilni glasovi porastu za samo 5 procentnih poena, dok se u drugoj opštini to uopšte ne dešava, to je jasan pokazatelj da je fokus manipulacije u prvom slučaju.
4. Kombinujte kvantitativne i kvalitativne dokaze.
   Statistički modeli mogu pokazati obrasce, ali tek kada ih posmatrači potvrde na terenu (npr. pritisci na birače, nepravilnosti kod mobilnog glasanja), nalazi postaju neoborivi.
5. Koristite rezultate za targetirano posmatranje.
   Logit/probit analize mogu pomoći da se identifikuju „rizična“ biračka mesta gde su šanse za nepravilnosti najveće. Posmatračke misije tako mogu efikasnije rasporediti resurse i obratiti posebnu pažnju na problematične lokacije.

---

👉 Ukratko: Logit i probit modeli nisu samo akademski alati, već i praktični instrumenti za unapređenje kvaliteta posmatranja. Oni pomažu da se brojke prevedu u „kvote“ koje su lako razumljive i analitičarima i široj javnosti.

---

Panel regresije – intuitivna osnova

Koriste se kada imamo podatke kroz vreme i prostor (npr. iste opštine kroz 10 godina).
Primer: Ako se veza između mobilnih glasova i rezultata SNS-a povećava kroz više ciklusa, to može ukazivati na dugoročnu sistemsku praksu manipulacije.

Moguća pitanja za napredne modele u forenzici izbori

Logit/Probit modeli:

• Kolika je verovatnoća da SNS osvoji više od 60% glasova na biračkom mestu kada je udeo glasova van biračkog mesta veći od 5%?
• Da li prisustvo velikog broja nevažećih listića smanjuje verovatnoću da opozicione liste pređu cenzus?
• Kako se verovatnoća uspeha kvazi-opozicionih lista menja sa porastom izlaznosti?

Panel regresije:

• Da li se veza između izlaznosti i glasova za SNS u istoj opštini menja tokom više izbornih ciklusa?
• Da li opštine sa visokim procentom mobilnog glasanja na prethodnim izborima pokazuju iste obrasce i u sledećem ciklusu?
• Kako se obrasci manipulacija razlikuju između urbanih i ruralnih sredina kroz vreme?

---

5. Zaključci i preporuke za posmatrače

Regresiona analiza je snažan alat jer omogućava posmatračima da kvantifikuju odnose između izbornih pokazatelja. Na osnovu primera iz Kosjerića i Zaječara, jasno je da mobilno glasanje predstavlja najvažniji faktor povezan sa prednošću vladajuće stranke.

• Korelacije su brze i pregledne, ali regresija ide dalje, daje procene koliko tačno jedan faktor utiče na rezultate.
• \(R^2\) je ključan indikator: pokazuje koliko model objašnjava varijacije. Kada je \(R^2\) visok (0,8), posmatrači znaju da je odnos vrlo snažan. Kada je nizak (0,26), to znači da postoje i drugi faktori koje treba istražiti.
• Mobilni glasovi su najopasniji indikator manipulacija. Pozitivna i značajna veza s rezultatima SNS-a u oba grada jasno sugeriše zloupotrebu.
• Nevažeći listići su još jedan signal. U Kosjeriću manji broj nevažećih je povezan s više glasova za SNS, što može značiti da je kontrola biračkih listića bila prilagođena u korist vlasti.
• Izlaznost se pokazuje kao neutralna. Njena beznačajnost u modelima sugeriše da nije sama po sebi odlučujući faktor, već je ključ u specifičnim kanalima poput mobilnog glasanja.

Preporuke

Posmatrači treba da se fokusiraju na biračka mesta sa velikim udelom mobilnih glasova i na obrasce vezane za nevažeće listiće. Regresione analize treba kombinovati sa posmatračkim izveštajima sa terena, samo tako se može potvrditi da brojke odražavaju realne manipulacije. Objavljivanje rezultata regresija u izveštajima (sa tabelama i grafikama) značajno povećava kredibilitet posmatrača i doprinosi javnom razumevanju izbornih nepravilnosti.