1. Uvod

Benfordov zakon je matematičko pravilo koje opisuje raspodelu vodećih cifara u mnogim prirodnim i društvenim skupovima podataka. Prema ovom zakonu, manji brojevi (posebno cifra „1“) pojavljuju se kao prva cifra znatno češće od većih brojeva („9“). Iako na prvi pogled zvuči kontraintuitivno, Benfordov zakon ima široku primenu u detekciji nepravilnosti – od finansijskih podataka, preko naučnih baza, do izbornih rezultata.

U forenzici izbora, Benfordov zakon koristi se kao alat za prepoznavanje potencijalnih anomalija u brojevima glasova. Ako raspodela vodećih cifara značajno odstupa od očekivanog obrasca, to može biti signal da su rezultati manipulativno menjani.

2. Teorijska i intuitivna osnova

Zašto se Benfordov zakon javlja? Ideja je jednostavna: u brojevima koji nastaju prirodnim procesima (rast populacije, veličina firmi, izborni rezultati u velikim jedinicama), cifre nisu ravnomerno raspodeljene. Brojevi koji počinju s „1“ javljaju se češće jer prelazak iz 1 u 2 zahteva manji relativni porast nego prelazak iz 8 u 9.

Intuitivan primer: ako broj birača raste od 100 do 200, sve vrednosti imaju prvu cifru „1“. Ali od 800 do 900, sve vrednosti počinju s „8“. Dakle, „1“ pokriva širi opseg brojeva nego „8“ i zbog toga se javlja češće. Na prvi pogled izgleda da i „1“ i „8“ pokrivaju isti apsolutni opseg (100 brojeva: 100–199 i 800–899). I to je tačno! Ali ključ Benfordovog zakona nije u apsolutnim opsezima, nego u relativnim opsezima u logaritamskoj skali.

Zašto je „1“ češća prva cifra od „8“?

• Kada gledamo brojeve koji rastu kroz više redova veličine (10, 100, 1000, …), cifra „1“ zauzima veći deo logaritamskog prostora.
• Na primer, svi brojevi od 1 do 9:
  • „1“ zauzima interval 1–2 → to je 100% rasta (dupliranje).
  • „8“ zauzima interval 8–9 → to je samo 12,5% rasta.

Drugim rečima:

• Brojevi sa „1“ kao prvom cifrom javljaju se svaki put kada prelazimo pragove 1→2, 10→20, 100→200, 1000→2000 itd.
• Brojevi sa „8“ javljaju se tek kada prelazimo pragove 8→9, 80→90, 800→900, 8000→9000…

Zato je mnogo veća šansa da u prirodnim ili društvenim procesima (koji rastu multiplikativno, u relativnim skokovima) dobijemo broj koji počinje sa „1“ nego sa „8“.

---

Formalno objašnjenje

Benfordov zakon kaže da je verovatnoća da prva cifra bude: \(P(d) = \log_{10}\bigg(1 + \frac{1}{d}\bigg)\)

• Za \(d=1: P(1) = \log_{10}(2) \approx 30,1\%\)
• Za \(d=8: P(8) = \log_{10}(1+1/8) \approx 4,6\%\)

Dakle, iako oba „pokrivaju“ 100 brojeva u jednom intervalu, njihovo relativno učešće u celom logaritamskom prostoru je potpuno različito.

---

👉 Ukratko: „1“ je češća prva cifra jer se češće javlja u relativnim, multiplikativnim intervalima rasta (dupliranja), dok „8“ pokriva mali deo tog prostora.

---

3. Primena u forenzici izbora

Benfordov zakon se prvobitno primenjivao na prvu cifru broja glasova koje je kandidat dobio na biračkim mestima. Potom se zakon koristio i na ostale cifre u testovima druge generacije. Teoretski, rasporedi prve četiri cifre treba da prate sledeće verovatnoće:

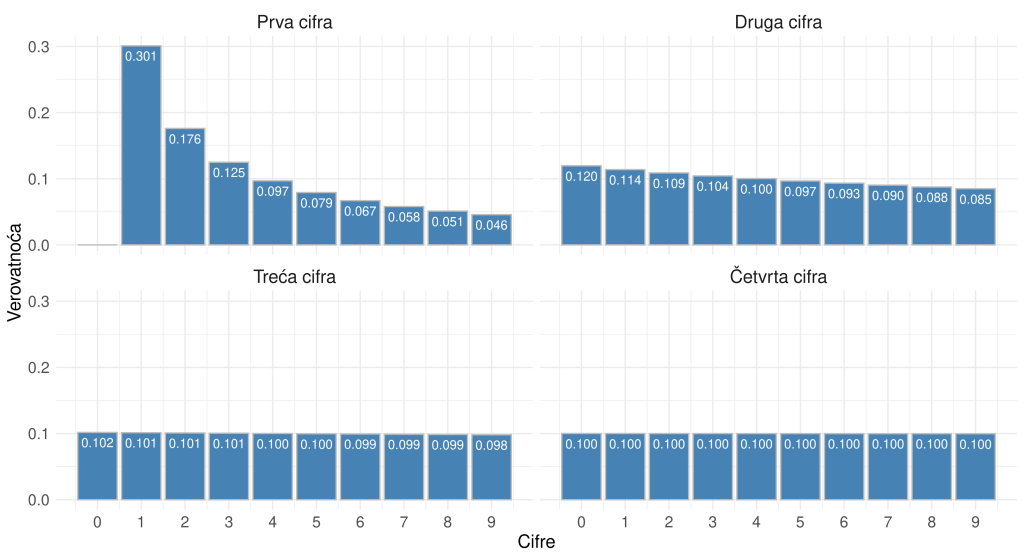
Da bismo proverili da li podaci slede ovaj raspored, koriste se statistički testovi, poput hi-kvadrat testa, test srednje vrednosti apsolutnih razlika (MAD test) i test luka mantise (MAT test) O primeni ovih i drugih testova koji se odnose na Benfordov zakon može se pročitati u knjizi Kovačić (2024).

Zašto broj glasova po biračkim mestima može da prati Benfordov zakon?

Zamisli da posmatramo opštine ili biračka mesta različite veličine. U manjim selima izlazi 300–400 ljudi, u gradskim mestima 2000–3000, a u velikim centrima 5000–6000 birača. Kada se sabere veliki broj ovakvih jedinica, dobijamo raspored koji obuhvata više redova veličine (stotine, hiljade, desetine hiljada glasova).

• Ako se glasovi raspoređuju „prirodno“, onda prva cifra može biti 1, 2, 3… sve do 9.
• Ali po logici Benfordovog zakona cifre 1, 2 i 3 javljaju se češće jer pokrivaju veći deo logaritamskog prostora rasta.
• Na primer:
  • Brojevi 1000–1999 → svi počinju s „1“.
  • Brojevi 8000–8999 → svi počinju s „8“.
  • Pošto se biračka mesta češće „nalaze“ u donjem delu skale (manja i srednja veličina), biće i više brojeva koji počinju sa „1“ ili „2“.

---

Kada podaci ne bi trebalo da prate Benfordov zakon?

Ako su sva biračka mesta približno iste veličine (npr. 700–800 glasova), tada prva cifra uvek pada u opseg „7“ ili „8“. Tu Benfordov zakon nije primenljiv, jer nema dovoljno raspona brojeva. Ako su brojevi veštački generisani ili zaokruženi (npr. 1500, 2000, 2500), poslednje cifre će pokazivati neprirodan obrazac (previše nula ili petica). Ako se u rezultatima pojavljuje nenormalno veliki broj „lepih brojeva“ (npr. 500, 1500, 2000 glasova), to može biti znak da su podaci „doterivani“.

---

👉 Dakle:

• Normalno: ako pogledamo sve biračke jedinice jedne zemlje, prva cifra broja glasova bi trebalo da prati Benfordov raspored.
• Sumnjivo: ako prva cifra (ili poslednja cifra) odstupa, npr. previše glasova se završava na 0 ili 5, ili su „8“ i „9“ mnogo češći nego što bi trebalo, to može biti signal moguće manipulacije.

---

4. Testovi druge generacije

Iako je analiza prve cifre najpoznatija, savremena forenzika izbora razvila je dodatne testove koji se oslanjaju na Benfordov zakon ili na sličnu logiku.

• 2BL (Second-digit Benford Law): analizira raspodelu druge cifre. Prosečna vrednost druge cifre trebalo bi da bude blizu očekivane vrednosti od 4,187.
• LastC: prosečna vrednost poslednje cifre glasova (očekivana vrednost je 4,5). Prirodno se očekuje uniformna raspodela (videti Sliku 1).
• C05: broj biračkih jedinica gde se glasovi pobednika završavaju na „0“ ili „5“. Nenormalno visok broj takvih slučajeva može sugerisati zaokruživanje ili „štelovanje“. Očekivana vrednost ove binarne promenljive je 0,2.
• P05: procenat biračkih mesta gde glasovi opozicionih kandidata završavaju na „0“ ili „5“. Očekivana vrednost u slučaju poštenih i slobodnih izbora bez strateškog glasanja je 0,2.
• DipT (Dip test): proverava da li raspored izlaznosti ima više od jednog „vrha“. Prirodno se očekuje unimodalni raspored.
• Skew: meri asimetričnost rasporeda izlaznosti. Velike pozitivne ili negativne vrednosti mogu ukazivati na neuobičajene obrasce mobilizacije.
• Kurt: meri „spljoštenost“ rasporeda izlaznosti. Nenormalno „šiljast“ ili „ravan“ raspored može ukazivati na manipulacije.

Ovi testovi pomažu da se sagleda šira slika i identifikuju anomalije koje sama analiza prve cifre možda ne bi otkrila. Detaljnije o intuitivnom objašnjenju ovih testova i njihovoj primenu na rezultate izbora u Srbiji može se pročitati kod Hicken & Mebane (2017) i u knjizi Kovačić (2024).

---

5. Ograničenja i kritike

Iako je Benfordov zakon moćan alat, njegova primena u forenzici izbora ima ograničenja:

• Veličina uzorka: Na malim uzorcima ili malim biračkim mestima raspored može prirodno odstupati.
• Raspon podataka: Ako brojevi glasova nemaju dovoljan opseg (npr. svi su između 100 i 300), raspored cifara neće slediti Benfordov zakon.
• Lažno pozitivni signali: Odstupanja ne moraju nužno značiti manipulaciju – mogu biti posledica demografskih ili geografskih specifičnosti.

U literaturi se često ističe da Benfordova analiza može biti korisna kao signal upozorenja, ali ne i kao „konačan dokaz“ izborne krađe. Zato se mora kombinovati sa drugim statističkim testovima i terenskim posmatranjem.

---

6. Praktična komponenta

✅ Excel

1. Uneti broj glasova po biračkim mestima.
2. Izdvojiti prvu cifru pomoću formule: =LEFT(A2,1)
3. Izračunati učestalost svake cifre od 1 do 9.
4. Porediti dobijene procente sa Benfordovim očekivanim vrednostima.
5. Primeniti hi-kvadrat test pomoću funkcije CHISQ.TEST.

Negrini (2012) je uz svoju knjigu na temu računovodstvene forenzike priložio Excel fajl koji omogućava primenu važnijih testova na osnovu Benfordovog zakona. Dovoljno je u tabeli Data uneti sirove podatke, da bi se automatski dobili svi rezultati testova kao i pripadajući grafici. Modifikovana verzija tog fajla može se ovde preuzeti.

✅ R

# Učitavanje podataka
data <- read.CSV("izbori.CSV")

# Ekstrakcija prve cifre
first_digit <- substr(data$glasovi, 1, 1)
first_digit <- as.numeric(first_digit)

# Učestalosti
table(first_digit)/length(first_digit)

# Test prve cifre (hi-kvadrat)
expected <- c(0.301,0.176,0.125,0.097,0.079,0.067,0.058,0.051,0.046) * length(first_digit)
chisq.test(table(first_digit), p=expected/sum(expected))

# Analiza druge cifre
second_digit <- as.numeric(substr(data$glasovi, 2, 2))
mean(second_digit, na.rm=TRUE)

Ovaj kôd omogućava da se brzo proveri da li podaci prate Benfordov raspored i da se urade dodatne analize.

Za R program razvijeno je nekoliko paketa koji omogućavaju proveru da li podaci slede Benfordov zakon. Najvažniji je benford.analysis paket koji omogućava numeričku i grafičku analizu podataka i identifikaciju sumnjivih podataka koji značajno odstupaju od Benfordovog zakona.

Ovde dajemo primer grafičkog rezultata analize predsedničkih izbora u Srbiji 2022. godine za kandidata Aleksandra Vučića. Detaljnija analiza ovih rezultata data je u knjizi Kovačić (2024).

---

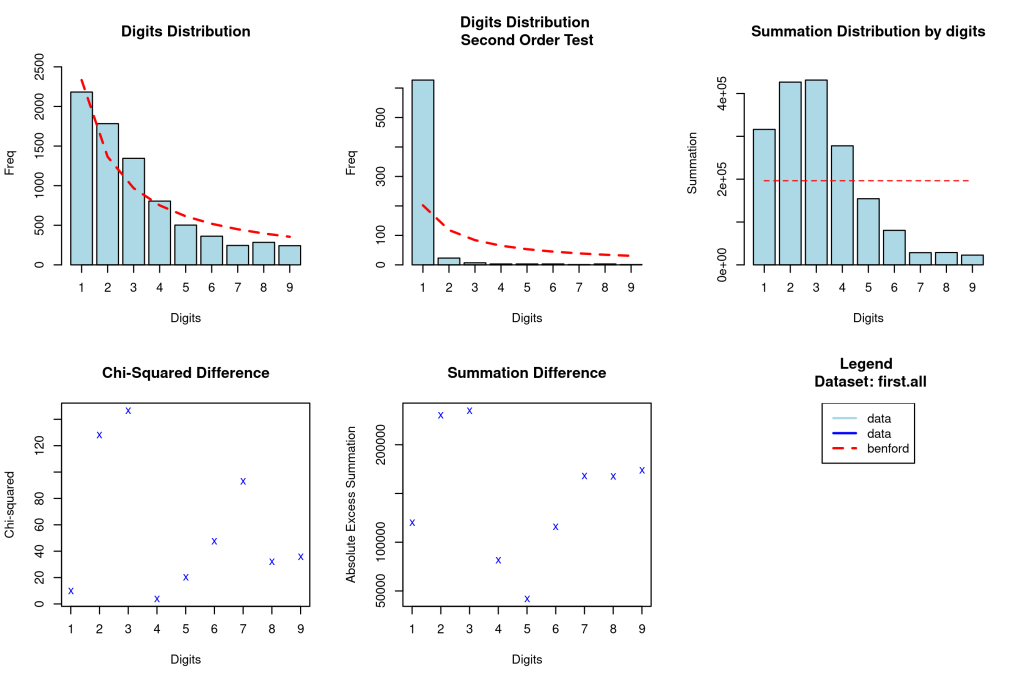
7. Analiza slučaja: Predsednički izbori u Srbiji 2022. godine

Kontekst

Na predsedničkim izborima u Srbiji 2022. godine pobedio je Aleksandar Vučić (SNS) sa 58,65% glasova na nacionalnom nivou. Kao i u mnogim drugim izborima u regionu, postavljalo se pitanje integriteta rezultata i da li statističke metode, poput Benfordovog zakona, mogu da otkriju anomalije u izlaznosti i broju glasova po biračkim mestima.

---

Analiza prve cifre

Raspored prve cifre glasova za kandidata Aleksandra Vučića dat je na Slici 3.

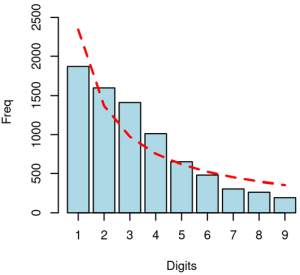
Kada se posmatra raspored prve cifre broja glasova za Vučića na svim biračkim mestima može se zaključiti sledeće:

• Za raspored prve cifre izbornih rezultata ovog kandidata na osnovu MAD testa može se reći da je neusaglašen sa rasporedom prve cifre prema Benfordovom zakonu.
• „1“ je bila najčešća prva cifra, što je u skladu sa prirodnom logaritamskom raspodelom, no znatno manja od očekivane vrednosti (isprekidana crvena kriva). Za razliku od toga, cifre “3” i “4” su se javljale znatno više nego što je pretpostavljeno na osnovu Benfordovog zakona (pozitivno odstupanje).
• Napominjemo da na osnovu testa i grafičke analize ne sledi da je u slučaju ovog kandidata bilo izbornih manipulacija, ali ovakav zaključak šalje nam upozoravajući signal da ima osnova ispitati ove rezultate izbora drugim metodama koje bi ukazale na poreklo ovakvog rezultata.

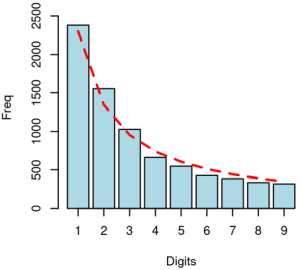
Za glavnog opozicionog kandidata (Zdravko Ponoš) raspodela prve cifre (Slika 4) bila je nešto ravnomernija, ali su se uočila manja odstupanja kod cifara „4“ i „8“ (negativna odstupanja) i kod cifara “1” i “2” (pozitivna odstupanja), što može ukazivati na specifične demografske obrasce ili na nepravilnosti. MAD test je ukazao na to da se može prihvatiti hipoteza da raspored prve cifre izbornih rezultata ovog kandidata sledi Benfordov zakon.

---

Testovi druge generacije

Primena dodatnih testova na broj glasova za Vučića na svim biračkim mestima otkrila je sledeće (detalji u knjizi Kovačić (2024)):

• 2BL test: test srednje vrednosti druge cifre izlaznosti odbacio je hipotezu da je ona jednaka očekivanoj vrednosti. Ovaj rezultat je indikator mogućih izbornih manipulacija.
• DipT (unimodalnost izlaznosti): raspored izlaznosti po biračkim mestima generalno je bio unimodalan, ali su na velikim biralištima kod rasporeda glasova pobednika zabeleženi dodatni „vrhovi“, što može upućivati na ciljanu mobilizaciju.
• Skew test: raspored izlaznosti pokazao je blagu pozitivnu asimetriju (više biračkih mesta sa visokom izlaznošću nego što se očekuje) u većem broju okruga.

---

Tumačenje i implikacije

Rezultati Benfordove analize za predsedničke izbore 2022. u Srbiji ne ukazuju na masovnu i sistematsku manipulaciju na nivou cele zemlje, raspodela cifara je uglavnom sledila očekivane obrasce. Međutim, lokalne anomalije po okruzima i veličini biračkog mesta (posebno kod druge cifre i izlaznosti) pokazuju da izborni rezultati zaslužuju detaljnije ispitivanje.

Za posmatrače i analitičare, ključna poruka je da Benfordov zakon može pomoći da se brzo identifikuju „sumnjiva mesta“ – ali da uvek treba kombinovati ovu analizu sa drugim metodama i terenskim posmatranjem.

8. Zaključci i preporuke za posmatrače

1. Benfordova analiza je brza i jednostavna alatka koja može signalizirati mesta sa potencijalnim anomalijama.
2. Analiza prve cifre često daje prvi signal, ali testovi druge generacije (2BL, LastC, C05, P05, DipT, Skew, Kurt) omogućavaju dublji uvid.
3. Rezultate treba tumačiti pažljivo, odstupanja mogu biti rezultat demografskih razlika, a ne nužno manipulacije.
4. Najbolja praksa je kombinovati Benfordovu analizu sa drugim metodama (npr. korelacionim i regresionim analizama, analizom izlaznosti, geografskim obrascima) i sa posmatračkim izveštajima sa terena.

👉 Ukratko: Benfordov zakon ne daje konačan odgovor, ali jeste dragocen „filter“ kojim posmatrači mogu da identifikuju sumnjive obrasce i usmere pažnju tamo gde su rizici najveći.

Literatura

Hicken, A., & Mebane, W. R. Jr (2017). A guide to election forensics. Preuzeto sa https://www.iie.org/wp-content/uploads/2023/01/UM-Election-Forensics-Guide-FINAL.pdf

Kovačić, Z. J. (2024). Forenzička analiza izbora u Srbiji – Predsednički, parlamentarni i lokalni izbori. Orion-arts books. https://bit.ly/m/Zlatko

Negrini, M. J. (2012). Benford's law: Applications for forensic accounting, auditing and fraud detection. New York: John Wiley & Sons.